下篇我们将重点介绍压电性介质中的各种弹性波模式，正式开启这场机电耦合与波动工程结合之旅。将从两个方面进行介绍：声表面波类和体声波类。

正式介绍前要说明下：固体介质中弹性波的传播涉及到原子的相对位置的改变，一般用应变来定量地描述这种改变。位置变化可以用原子保持的平衡状态被打破而产生的位移来表示(位移是位置的函数)。在存在应变的情况下，介质产生的内力具有使原子恢复到无应变的平衡状态的趋势，这个内力可以用应力来表示。所以，弹性波的传播会涉及到应力和应变这两个物理量，我们在后文描述弹性波模式时采用位移场振型和应力场振型。其次，在非压电性材料体系中，我们知道弹性波有三个主要分量L(纵波)、SV(垂直剪切波)、SH(水平剪切波)；而在压电性材料体系中还会增加一个电势Ф分量。

1. 声表面波模式

 (1). Rayleigh 波

Rayleigh波的振动方式兼有纵波和横波的特点，类似于质点做圆周式振动的水波，其扰动局限于一个厚度与波长相当的表面区域。在介质表面附近纵波(L)和垂直剪切波(SV)发生耦合，构成一个简正模，其中纵波与垂直剪切波相位差π/2，在介质中质点呈椭圆轨迹运动，其在介质中的传播如图15-16 所示：Rayleigh波沿垂直于介质厚度方向向下传播，振幅呈指数形式衰减，声波能量主要集中在表面 1~2 个波长范围内，粒子位移主要是纵向的。

其波速度可以用如下公式近似表示：

(ν 泊松比、vSH/SV水平剪切/垂直剪切波速)

Rayleigh波能量与介质深度的关系为，其中满足：

(ζ衰减常数，βs波数， 透射到介质中的深度)

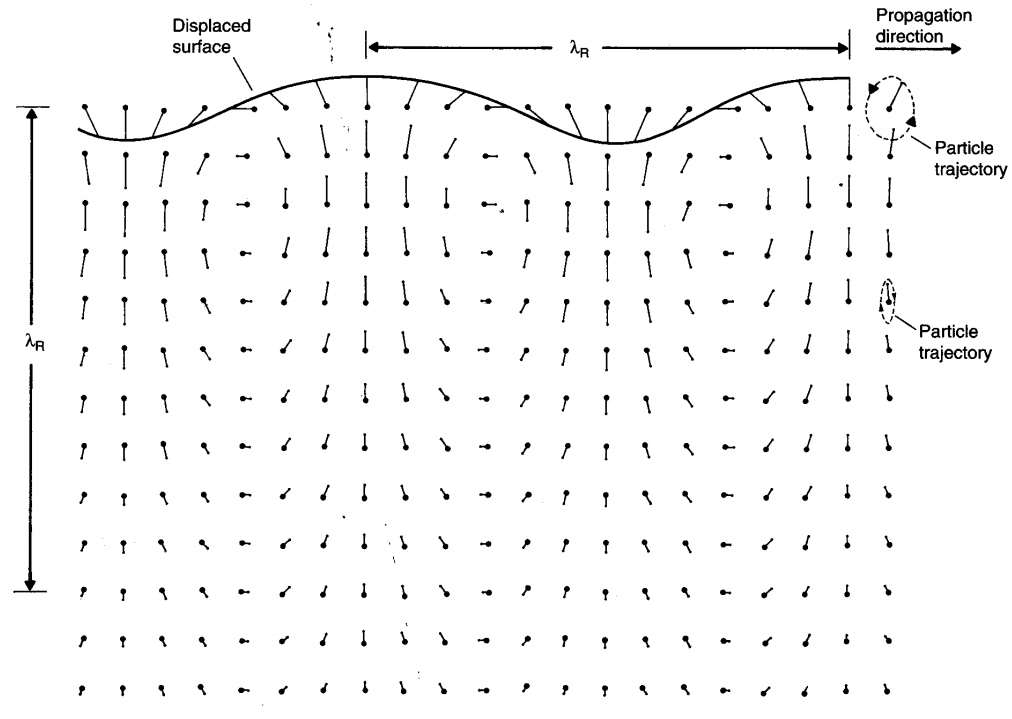
图15 Rayleigh波的场分布：介质中质点呈椭圆轨迹运动

图16 Rayleigh波在介质中的传播示意图

Rayleigh波的波速一般只决定于传播介质的材料参数，而与频率无关，即为非色散波(非绝对情况，如AlN层状结构中，会随着AlN的厚度而发生变化。类Rayleigh波)。在离表面为 0.2 个波长的深度以下，其运动方向与表层相反。在自由表面上，质点沿表面法向的位移约为切向的 1.5 倍。Rayleigh波能够激发的压电性材料体系：石英、部分切型的LiNbO3(TCSAW, Temperature Compensation Surface Acoustic Wave)、AlN、ZnO、PZT等；在一些含有LiNbO3压电材料的体系中是以寄生模的形式被激发的。其次，还有部分材料体系中(如(11-20)ZnO/R-sapphire[0001])除了激发基态Rayleigh波外还会存在高阶Rayleigh波模态，如图18所示。

图17 Rayleigh波的位移场分布(包括对称型和反对称型)

图18 高阶（1st）Rayleigh波的位移场分布

注：简正模(normal mode)是一个震荡系统中所有部分都以相同的频率和相位以正弦函数形式运动的模式。由简正模描述的自由运动发生在固有频率频率上，一个系统的一般的运动可以写成其简正模的叠加，但之所以称之为“简正的”，是因为它们可以独立运动，即给物体施加一种模的激发，永远不会导致物体以另外一种模运动，简正模彼此“正交”。

 (2). SH 波

对于压电声学器件领域的从业人员，对于SH型声波模式是非常熟悉的，它是声学滤波器中很重要的一种工作模态。首先，我们知道SH波属于S波(剪切波)的一个分量，弹性介质发生切变时所产生的波动。剪切形变在介质中传播，质点的振动方向(沿y轴，且振动方向与传播面平行)与波动的传播方向(x轴)垂直，即水平剪切横波。S波还有另外一个分量---SV波，质点的振动方向(沿着z轴，且振动方向垂直于传播面) 与波传播方向(x轴)垂直，即垂直剪切横波，它的特点在于，其振动方向垂直于波的传播方向，而在传播面内没有水平方向的分量。

线性源激励时，SH波满足表面边界条件，体声波以相同的振幅沿着各个方向传播，包括与介质表面平行的方向，所以SH波既可以在介质表面传播也可以在介质体内传播。在体内传播时弹性波的振幅以1/sqrt(r)形式递减(L波和SV波也同)，如图19所示，各个波的分量不会在体内相互耦合。在压电性材料体系中，体声波可以与电势Ф相互耦合，当SH波的场分量与电势Ф耦合后就会形成一种SH型的声表面波，它同时满足压电介质表面的机械边界条件和电学边界条件。SH型声表面波的场分布也可以用公式(2)决定，它的波速比SH型体声波的波速慢，SH 型声表面波声速的下降情况反映出压电介质表面压电性的强度(机电耦合的强度)。随着波速下降，SH 型声表面波的能量逐渐集中在介质表面(随SH声表面波压电性增强，电学表面边界条件的影响越来越明显，声波能量逐渐集中在介质表面)。

图19 平面上线性源激励的体声波辐射模型

图20 SH波的位移场分布(包括表面波型和体声波型)

通常压电材料是各向异性的，在压电介质中的SH分量和电势Ф都可以与L波分量和SV波分量相互耦合，所以严格来说，前面描述的Rayleigh波和SH声表面波包含有三个机械波分量和电势Ф，即Rayleigh波和SH声表面波分别是以准Rayleigh波和准SH声表面波的形式在压电介质中传播，这两种波模式在不同的材料体系和不同方向上存在“漏”与“非漏”两种类型(“漏”与“非漏”的判断本文将不再展开描述，感兴趣的朋友可以阅读相关文献)。此处简要介绍下我们熟知的NSAW(Normal Surface Acoustic Wave)中的工作模态漏SH声表面波(也叫表面横波STW)，在各向异性压电体中慢剪切SH型体波的波速比准Rayleigh波的波速慢，从公式(2)可以看出，SH波分量的能量将不再集中在压电介质表面附近，其能量在波传播过程中会泄露到介质内部，在介质表面上的振幅呈指数形式衰减。这种能量沿着压电介质厚度方向泄露衰减现象会导致声表面波器件的Q值发生恶化，这也催生了我们熟悉的IHP-SAW (或TF-SAW, Thin Film Surface Acoustic Wave)技术：如图21所示，通过高低声阻抗层(形成Bragg反射层)将泄露的能量束缚在压电介质表面或压电介质层中，从而使得声表面波器件的Q值得到大幅提升。

图21 位移场分布：(a)NSAW(42°YX-LT)，(b) IHPSAW(LT/SiO2/AlN/Si)

SH型声表面波能够激发的压电性材料体系：LiTaO3(NSAW)、部分切型的LiNbO3(TCSAW)、LT层状结构(TFSAW/TCSAW)等；还有部分压电性材料体系中也能够被激发，但它是以寄生模的形式存在。

(3). Love 波

通常，在压电介质上沉积一层慢剪切波波速的材料时，可以激发起一种简正模的SH型声表面波(即为Love波)。Love波的振动和传播形式与SH波一致，质点的振动平行于弹性介质表面(传播面)，振动方向(y轴)与传播方向(x轴)垂直，其传播像是一种蛇形前进的横向波动，传播过程中会产生剪切位移，其振幅比横波大，振幅随着深度的增加而衰减(当表层较薄时，会出现很强的Love波)。

图22 Love波在介质中的传播示意图

Love波存在的条件是波的传播速度要小于半空间的体剪切波速而大于层的体剪切波速。由于Love波是在波导层中传播，其在压电介质厚度方向上的质点位移分量为0，所以Love波器件中声波的能量几乎全部聚集在波导层中，对表面干扰非常灵敏(很多传感器采用Love波作为工作模态)。Love波位移场分布如图23所示。

图23 Love波的位移场分布(包括对称型和反对称型)

Love波能够激发的压电性材料体系：LiTaO3、LiNbO3、石英等等；在SAW谐振器/滤波器中，Cu电极加载在低旋切角(如0°、5°、10°、15°等)YX LiNbO3材料体系中可以激发出具有超高机电耦合系数的Love波模式。Love 波也存在高阶模态，在某些材料体系中(如(1120)ZnO/R-sapphire[1100])，除了能够激发基态Love波外还会在高频侧出现高阶的Love波模式，如图24所示。

(a) 0th Love波                                                            (b) 1st Love波

图24 Love波的位移场分布

 (4). Stoneley波

Stoneley波也是一种在弹性介质界面传播的波，由沿界面传播的非均匀的P波和S波合成，沿界面方向传播的波速小于两个介质中最小的剪切波波速，沿垂直于界面的两个方向以不同的指数规律衰减。是一种波速与两个介质的性质相关的类瑞利波的波模态(“变态”瑞利波)。

图25 压电材料和各向同性材料的结构

若界面为X2=0，对于X1-X3平面内传播的二维P波和S波分量，其位移势函数可分别假设为与瑞利波类似的形式：

带入到波动方程，由界面的位移和面力连续条件得到一个特征值问题，用于确定存在的Stoneley波的波速CSt的特征方程。可以发现，只有在两种介质的材料参数满足一定条件的情况下才存在Stoneley波，即特征方程使有实数解。

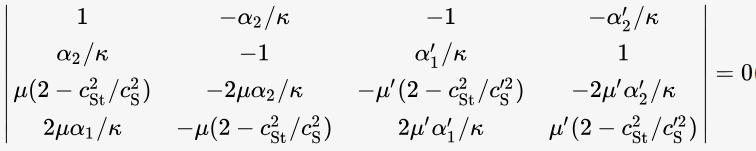
Stoneley波传播过程中的位移场分布，如图26所示。

图26 有限振幅下的Stoneley波场分布

Stoneley波常见于压电材料与各向同性材料形成的交界面，如图27为典型材料体系下的Stoneley波存在的参数范围。在声表面波器件中比较少见，即使存在也是一般以寄生模态形式存在。

图27 Stoneley波的存在范围 

 (5). Sezawa波

地震学家 Sezawa 和 Kanai 于 1935 年(出现在他们关于瑞利波色散曲线不连续性的论文中)发现了 Sezawa 波。他们认为在给定刚度比率和泊松比率的每种情况下，除了地层中有许多水平节面的波外，应该只有一条色散曲线，但实际计算发现(即使比率为 1/5)会有两条不同类型的波的色散曲线。如图28所示，图中的曲线 AB 是典型的Rayleigh波，而 CD 是另一个新的模式的波，这个波就是Sezawa波。

图28 不同比率下的弹性波的色散曲线(其中CD为Sezawa波)

在声表面波器件中，Sezawa波与Rayleigh波相同，也是通过压电效应产生的，这种泛音声学传播(泛音是指在加强基频的同时，还伴随着一系列高音谐波的声音)模式一般出现在更高的频率上，又将其称为“高阶Rayleigh波”。Sezawa波仅在归一化压电层厚度的特定值范围内进行激励，其波速与归一化压电层厚度 h/λ 之间存在色散关系，波速的增加或减少取决于压电层相对于子层的声学特性。当 h/λ 高于 1 左右的临界值时，只有一条色散曲线(与Rayleigh波相关)，其中声波能量局限于压电层(顶层)；当 h/λ 低于该临界值时，声波能量会透过压电层进入到子层中。在第二种情况下，当压电层中的波速低于子层的波速时，压电层的弯曲和拉伸运动与子层中的表面扰动相互耦合产生 Sezawa 波模式。所以，Sezawa 波存在的条件是层叠的压电层的声波相速度低于子层的声波相速度。其Sezawa波传播过程中的位移场分布如图29所示

(a)AlN/Si                                                            (b)ZnO/Si

图29 Sezawa波的位移场分布

(6). Leaky波

漏波(Leaky-SAW)最早由H. Engan等人发现的，他们在各向异性介质α-石英的某些方向上观察到了两种相速度不同的表面波。其中一种在传播过程中向体内辐射体波而衰减，因此称为漏(表面)波。如图30所示。

通常认为，对任何材料的任何切向，均有唯一的Rayleigh波解存在， 但对Leaky波来说却不是这样，它只存在于部分材料的某些切向上，人们以寻找在哪种材料的哪些切向上的Leaky波具有低传播损耗、高机电耦合系数、高的传播速度和低的温度系数等，典型的如41°YX -LiNbO3、36°YX -LiTaO3等。

在特定的材料体系和边界条件下，许多其他类型的声表面波模态都可以成为漏波。一般情况下，当声表面波的波速比慢剪切体声波的波速大时，就会存在漏声表面波。

(a) x平面          (b) y平面           (c) z平面

图30 表面波的相速度 Ⅰ普通表面波，Ⅱ漏表面波，Ⅲ慢体积波

 (7). BGS (Bleustein-Gulyaev-Shimizu )波

BGS波(或称电声波)是一种在高对称性压电介质中存在的波，它是质点振动方向与传播方向垂直而与表面平行的切变波，而且是与电势耦合的一种表面波，它是一种的纯的SH波。即使压电介质没有较低速的表面层，也存在这种表面波。

BGS波是非漏波，我们前面讲到，一般当声表面波的波速比慢剪切体声波的波速大时，就会存在漏声表面波。但BGS波就是个特例，在激励BGS波的材料体系中，慢剪切体声波分量与其它分量是完全去耦的，这种去耦是由晶体结构的对称性引起的。当压电耦合不存在时，它就退化为切变体波。

BGS波最常出现在压电陶瓷或6mm晶体中，如YXlt/70°/90°石英、PZT等压电材料。

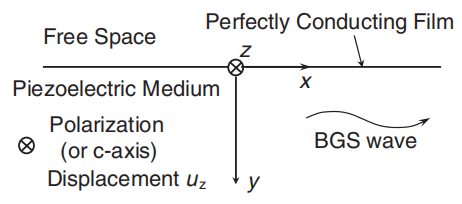
图31 金属化表面的半无限压电介质上的BGS波

图32 金属化表面BGS波粒子位移uz的深度分布

 (8). LLSAW波

LLSAW波是一种“漏”型的纵波，一般只在特定的压电材料及切型中激励。1995年Takahiro Stao和Hidenori Abe在具有4mm 晶体结构的材料---四硼酸锂(Li2B4O7)中发现LLSAW波，在其特定的旋转角上它的泊松比很小，也就是 SV 分量与L分量的相互耦合很小，因此存在一个主要由L分量和电势Ф分量耦合成的声表面波，人们将这种类型的声表面波称为纵向漏声表面波(Longitudinal-leaky-SAW，LLSAW) 。

LLSAW波相比普通的漏表面波具有更高的相速度，因此适合作为高频声表面波器件的工作模式。LLSAW波沿压电介质表面传播，波速介于在快速剪切波波速和纵波波速之间，在传播的过程中向介质体内辐射两种的剪切波。这种弹性波模式首先由Jhunjhunwala在理论上将其作为一种二阶伪声表面波(Pseudo SAW)而提出，但早期没有应用到器件上，因为它不像其他的漏声表面波那样，它有很高的传播损耗(很严重的体波辐射)。

图33 金属化表面的半无限压电介质上的LLSAW波

(a) 自由表面                       (b) 金属化表面

图34 LLSAW在LBO晶体中的位移和电势分布

LLSAW波除了在LBO晶体中可以激励外，还可以在特定切型的LiNbO3压电晶体中激励。近年来，基于LN压电材料的LLSAW波器件的研究异常火热，利用LLSAW模式的超高波速可以实现高频声学滤波器的开发，并且其还具有很高的机电耦合系数，可以实现高频大带宽滤波器的开发。LLSAW波在传播过程中有很严重能量泄露，会导致传播损耗很高，无法将滤波器的插入损耗(IL)做小。所以，研究者提出了两种解决思路：其一是在LN压电层下方设置高声速支撑衬底，高声速支撑衬底可以选择Si、蓝宝石、SIC、SiN、金刚石等等；其二是在LN压电层下方设置高低声阻抗层(Bragg反射层)，Bragg反射层可以选择SiO2、Ta2O5、HfO2、AlN、Ta、Pt、W、Ir等等。两种结构都是将泄露下来的能量束缚住，让其集中压电层表面或压电体内。两种结构的形式如35所示。

图35 LLSAW波器件结构

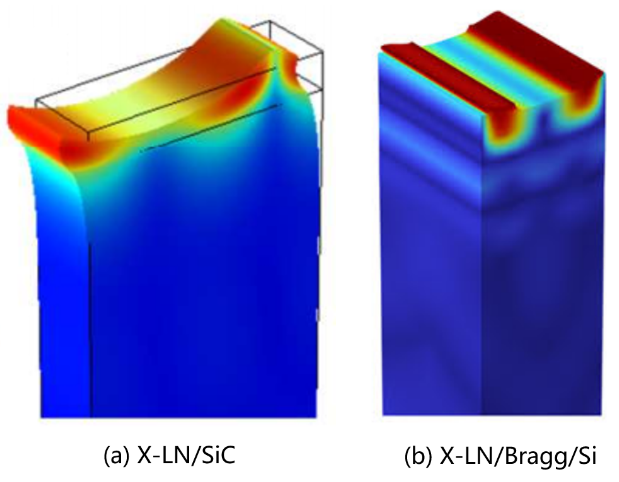
图36 LLSAW波的位移场分布

2. 体声波模式

体声波模式作为BAW谐振器/滤波器的工作模态，是另外一大类很重要的弹性波模态。利用通过大量体材料传播的声波模态，包括纵波、剪切水平（SH）波和剪切垂直（SV）波，其中纵向声波也称为P波，具有最高的相速度。BAW谐振器主要采用纵向模(Longitudinal mode)或厚度剪切模(Thickness Shear mode)。本文中将采用“弹性波模式在介质中具体的传播位置”原则来区分声表面波和体声波类型的(有的人是通过激励方式来区分的，不管用哪种方式都没毛病，所以不必纠结)。如图37所示，弹性波在不同结构中的传播示意图(右上为Plate Mode谐振器)。

所以，体声波模式部分将主要介绍如下几类弹性波模式：纵波和横波(简要介绍)、BAW模式、Lamb波、Lamé 波、SH0型plate波、高阶Lamb波(最近非常火热的XBAR的工作模态)等等。

图37 弹性波在不同结构中的传播示意图

(1). 纵波 (Longitudinal wave) 模式

纵波是波动的一种(波动分为横波和纵波)。纵波是质点的振动方向与传播方向同轴的波(或称平行)，常见的纵波有声波和地震引起的P波(P-waves，Primary wave)，亦称“疏密波”，传播过程是沿着波前进的方向出现疏密不同的部分(质点分布最密的位置叫做密部， 质点分布最疏的位置叫做疏部)，如图38所示。实质上，纵波的传播是由于介质中各体元发生压缩和拉伸的变形，并产生使体元恢复原状的纵向弹性力而实现的。因此纵波只能在拉伸压缩的弹性介质中传播，一般的固体、液体、气体都具有拉伸和压缩弹性，所以它们都能传递纵波。最早发现的纵波是声波，在声波在空气里传播时，由于空气微粒的振动方向与波的传播方向一致，所以是纵波。

图38 L(P)波在介质中的传播示意图

(2). 横波 (Transverse wave，或剪切波) 模式

横波是波动的一种(波动分为横波和纵波)。横波是质点的振动方向与波的传播方向垂直的波。由于质点的振动方向与波的传播方向相互垂直，在横波中突起的部分为波峰，凹下部分叫波谷，所以也称横波为“凹凸波”。波长通常是指相邻两个波峰或波谷之间的距离。在传播过程中，凡是横波传递到的地方，每个质点都在自己的平衡位置附近振动，由于波以有限的速度向前传播，所以后开始振动的质点比先开始振动的质点在步调上要落后一段时间，即存在一个位相差。这种传播在外表上看是一种“波浪起伏”，即形成波峰和波谷，传播的只是振动状态，媒质的质点并不随波前进。如图39所示。

实质上，横波的传播是由于媒质内部发生剪切变形(即是媒质各层之间发生平行于这些层的相对移动)并产生使体元恢复原状的剪切弹性力而实现的。否则一个体元的振动，不会牵动附近体元也动起来，离开平衡位置的体元，也不会在弹性力的作用下回到平衡位置。

图39 横波(S)在介质中的传播示意图

(3). BAW模式

薄膜BAW谐振器/滤波器是一种主要由被两个金属电极包围的压电薄膜组成的器件，这两个金属电极之间会产生根据厚度扩展模式(TE)传播的纵波。波被困在谐振器中的方法主要有两种，这就区分了目前已经大量制造的两种器件：薄膜体声谐振器(FBAR, Film Bulk Acoustic Resonator)和坚固安装谐振器(SMR, Solidly Mounted Resonator)。如图40所示为两种BAW谐振器的结构，这两种结构最大的不同是声波能量的束缚形式。

(a) SMR-BAW                                  (b) FBAR

图40 BAW谐振器示意图

BAW模式的激励模型，如41所示。考虑厚度为2d的压电材料板，以及位于板(或薄膜)的顶部和底部的无限薄电极。由于压电效应，在上下电极之间产生的电场在逆压电效应的作用下产生弹性波(体声波模式)，体声波在平板的厚度上传播。假设由于平板位于真空介质中，弹性波会因为机械波不能在真空中传播，所以在界面处反射。当入射波和反射波在结构内的某个地方相位叠加时，这种结构将产生机械共振。为了达到这个目的，平板厚度必须是共振频率下半波长的倍数。考虑波以声速v传播，则板的机械共振条件为：

其中n表示对应于每个半波长倍数的每个共振模式。

图41 厚度为2d的平板上的机械共振

事实上，压电驱动的谐振器它不会像上面那样工作。上面的情况只是一个纯机械系统，没有考虑到波的电激励。真正理解BAW谐振器的性质，需要描述控制压电谐振器的基本理论，需要与压电晶体的极化、力学和电畴的本构关系、牛顿第二定律、麦克斯韦方程等来联立起来解析，要理解其色散特性及等效传输线模型。(限于篇幅原因此处不再展开，感兴趣的朋友可以参阅相关文献去了解)

图42 BAW谐振器2D模型和电极和外部区域的色散曲线

BAW谐振器的有效耦合系数 Keff²的计算公式:Um弹性/Ud电性/Um互能。

在有真实电极的谐振器中，期望的Keff²可能与在理想的BAW中得到的不同，因为穿过压电层和电极的场模式将不满足下面的应力表达。在这种情况下，金属电极也在声学场发挥作用，因为声波能够传播到金属层中，如图43所示。

图43 具有与压电层厚度相当的电极的谐振器. 应力场(实线),位移(虚线)

对于上述这种简单的情况，有效机电耦合系数Keff²的表达式也可以为：

而更接近真实的情况是，与压电层相比，电极的声阻抗不同，如图44所示。在这种情况，不可能前面的公式推导出封闭形式表达式，因此需要采用数值方法。

图44电极厚度t且声阻抗高于压电层声阻抗的谐振器. 应力场(实线),位移(虚线)

下面将展示两种BAW谐振器的振型图(位移场分布)，如图45为SMR-BAW谐振器的，图46为FBAR谐振器的。

(a) 在厚度方向                                 (b) 顶面方向

图45 SMR-BAW位移场分布

(a) 在厚度方向                          (b) 顶面方向

图46 FBAR位移场分布

 (4). Lamb 波

Lamb波是当激励波波长与波导厚度处于同一数量级时，由横波和纵波耦合成的一种特殊形式的应力波，最常见的两种模态为：S模态(对称型)和A模态(反对称型)，对称型的Lamb波又称纵向板波(或膨胀板波)；反对称型的Lamb波则称为弯曲板波。Lamb波传播过程中，质点在平面内作类似于Rayleigh波那样的椭圆偏振运动。

Lamb波的解析是基于弹性力学的拉梅解的，波动方程分别用P波位移势φ和S波位移势ψ表示：假设波动位移与x2无关。

满足方程的解为：

其中待定的常数可以由上下表面的应力为零的边界条件来确定。由于兰姆波本质上是二维的，衰减更小，传播距离更长。

图47 板中(或薄膜)中Lamb波的形成过程

图48 对称和不对称Lamb波模态的示意图.Extensional, Flexural

兰姆波主要具备四个特性：频散、多模式、非稳态信号以及位变。频散是超声导波信号的固有属性，每种模式随着频率的变化，相速度和群速度都会随着频散特性作用发生变化；在高频条件下，零阶不对称Lamb模(A0)的波速接近Rayleigh波速，随着波长的减小，波模态逐渐转变为基态Rayleigh波(R0)或更高阶模式波。同样地S模态也会收敛于Rayleigh波模态。Lamb波与前面讲的Love波一样也存在高阶模，这些高阶模的质点振幅在板内的分布呈现为振荡状态，并且每种高阶模均有一特定的截止频率，当板厚一定时，只有频率达到该高次波的截止频率时，板内才能传播这种高阶模。

其次，在一些叠层状板(或薄膜)结构中，还会激发出准Lamb波(Quasi-Lamb wave)模态，由于压电层和其他材料层的材料特性使得Lamb波模式的位移分布相对于中性轴不是纯对称的(或者反对称的)，如图50所示，但Quasi-Lamb波的位移幅度与纯Lamb波(Pure-Lamb wave)相比几乎是相同。这种差异主要是由构成谐振器的板结构不同造成的。

图49 AlN压电材料体系

图50 常见的几种Lamb波模式

(5). Lamé 波

Lamé 波也属于Lamb波的范畴，只是激励性是有所区别，利用压电晶体(石英、LN等)特殊的取向，根据特殊方向上的极化进行弹性波激励，一般采用方形板4角固定安装，如图51所示为典型Lamé 波模式振型图。

图51  Lamé 波谐振器结构及Lamé 波的振型

图52 Lamé 波应力场分布

在这种类型的谐振器中，驱动谐振器中的横向振动的压电系数是d31。Lamé波与Lamb波一样也存在高阶模(高次谐波)，高次谐波是通过在谐振器的顶部形成一个交错的电极图案来激发的。只有当厚度与FP的比值很小时，才能实现纯粹的横向拉伸模态形状。同样的，Lamé波中也有准Lamé波模式(Quasi-Lamé-mode)与纯Lamé波模式(Pure-Lamé-mode)之分。

图53 Lamé 波高次谐波的位移场分布

(6).SH0板波

SH0板波也属于SH型体波的一种，其特性与SH波一致，这种类型的波既可以出现在薄板中，也可以出现在半无限及底中，激发条件此处不再详细描述。如图54所示为在不同结构中激发的SH0板波的位移场分布。

图54 SH0 板波位移场分布

(6). 高阶lamb波(XBAR)

近年来，压电声学器件领域研究最火热的方向非XBAR(laterally eXcited Bulk Acoustic wave Resonators)技术莫属。XBAR器件中的主要工作模态是Lamb波中的非对称模式A1模，一般都会采用高阶Lamb波模态作为工作模态，这些模态具有很高的波速和大的机电耦合系数，可以用于高频大带宽滤波器的设计开发。XBAR结构与BAW类似，同样具有两种：空腔型和固态装配型，不同处在于它的激发声波模态的电极采用叉指电极形式。

图55 XBAR谐振器结构及其工作模态

图56 XBAR 2D周期模型导纳曲线，包含XBAR模式和杂散模式。

图57 Lamb波的高阶非对称模式的位移场分布

(a)A1、(b)A2、(c)A3、(d)A4、(e)A5、(f)A6、(g)A7

3. 几种典型弹性波模式的电学响应

这部分内容我们将举几个简单的例子，不再进行一一介绍了。

（1）TCSAW：SiO2/Cu/LiNbO3材料体系中，主模为Rayleigh模，高频寄生的模式为Love模(SH)、Plate模，还有未显出的(或者被抑制掉的横向寄生模)。

图58 基于SiO2/Cu/LiNbO3的TCSAW谐振器的电学响应曲线

（2）TFSAW：Al/LiTaO3/SiO2/polySi/Si材料体系中，主模为SH波，高频寄生的模式为高阶体波，还有未显出的(或者被抑制掉的) 横向寄生模及截至体波。

图59 基于Al/LiTaO3/SiO2/polySi/Si的TFSAW谐振器的电学响应曲线

（3）BAW：AlN压电材料体系中，主模为体声波模式，还有寄生在谐振器禁带内的横向模。

图60 基于AlN的SMR-BAW(左)和FBAR(右)谐振器的电学响应曲线

总结

04

行文至此，这趟波动之旅就要接近尾声了，受限于篇幅和笔者的能力，还有许多内容无法一一描述，此文不尽不正之处，还望阅读此文的朋友能够指正。愿以此拙文能给关注压电声学器件领域的朋友提供一点帮助，同时也祝愿我们每个人的世界也如弹性波模态的世界一般精彩。

彩蛋：请各位读者猜猜这个“叠猫猫状”的模式是个什么弹性波模态？

参考文献：

[1] Lord Rayleigh (J. Strutt). On waves propagated along the plane surface of an elastic solid [J]. Proc. London Math. Soc, 1885.

[2] Ken-ya Hashimoto. Surface Acoustic Wave Devices in Telecommunications Modelling and Simulation [M]. Verlag Berlin Heidelberg: Springer, 2000.

[3] Lan, Xiaodong, et al. Simulation of SAW humidity sensors based on (11-20) ZnO/R-sapphire structures [J]. Sensors, 2016.

[4] Takai, Tsutomu, et al. IHP SAW technology and its application to microacoustic components [J]. 2017 IEEE International Ultrasonics Symposium (IUS), 2017.

[5] B.A. Auld. Acoustic Waves and Fields in Solids, Vol. II [M]. New York, 1973.

[6] A.E.H. Love. Some Problems of Geodynamics [J]. Dover, 1967.

[7] A.E.H. Love. Some problems of geodynamics [M]. Cambridge University, 1911.

[8] Shui, Yongan, and Igor Yu Solodov. Nonlinear properties of Rayleigh and Stoneley waves in solids [J]. Journal of applied physics, 1988.

[9] Irino, Toshio, Yasutaka Shimizu. Theoretical analysis of Stoneley waves propagating along an interface between piezoelectric material and isotropic material [J]. Electronics and Communications in Japan (Part II: Electronics), 1985.

[10] Katsutada Sezawa, Kiyoshi Kanai. Discontinuity in Dispersion Curves of Rayleigh-Waves [J]. 1935.

[11] Hadj-Larbi, Fayçal, Rafik Serhane. Sezawa SAW devices: Review of numerical-experimental studies and recent applications [J]. Sensors and Actuators A: Physical, 2019.

[12] Mohanan, Ajay Achath, et al. Investigation into mass loading sensitivity of sezawa wave mode-based surface acoustic wave sensors [J]. Sensors, 2013.

[13] Engan, H, K. A. Ingebrigtsen, A. Tonning. Elastic surface waves in α‐quartz observation of leaky surface waves [J]. Applied Physics Letters, 1967.

[14] Bleustein, Jeffrey L. A new surface wave in piezoelectric materials [J]. Applied Physics Letters, 1968.

[15] Gulyaev, Yu V. Electroacoustic surface waves in solids. Soviet Phys. JETP Lett, 1969.

[16] Nakamura, Kiyoshi. Shear-horizontal piezoelectric surface acoustic waves [J]. JJAP, 2007.

[17] Sato T, Hidenori Abe. Longitudinal leaky surface waves for high frequency SAW device applications [J].1995 IEEE Ultrasonics Symposium. Proceedings, 1995.

[18] Sato Takahiro, Hidenori Abe. Propagation properties of longitudinal leaky surface waves on lithium tetraborate [J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 1998.

[19] Morgan David. Surface acoustic wave filters: With applications to electronic communications and signal processing [M]. Academic Press, 2010.

[20] P. Zheng et al. Ultra-Low Loss and High Phase Velocity Acoustic Delay Lines in Lithium Niobate on Silicon Carbide Platform [J]. 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), 2022.

[21] T. Kimura et al. A High Velocity and Wideband SAW on a Thin LiNbO3 Plate Bonded on a Si Substrate in the SHF Range [J]. 2019 IEEE International Ultrasonics Symposium (IUS), 2019.

[22] Udaondo Guerrero, Carlos. Analysis of Q factor degradation mechanisms in BAW resonators. 2024.

[23] Zou, Jie. High-performance aluminum nitride Lamb wave resonators for RF front-end technology [M]. University of California, Berkeley, 2015.

[24] Johar, Arun Kishor, et al. Finite Element Modeling and Parametric Optimization of Solidly Mounted Film Bulk Acoustic Resonator for Its Performance Enhancement. 2021.

[25] J. Meltaus, T. Pensala, K. Kokkonen. Modelling of 2-D lateral modes in solidly-mounted BAW resonators [J]. 2008 IEEE Ultrasonics Symposium, 2008.

[26] Zhao, Zinan, et al. Lateral size-dependence in UHF mode-coupled ZnO FBARs to suppress undesirable eigen-modes and weaken mounting effect [J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2020.

[27] X Wu, J Cai. Design and modeling of film bulk acoustic resonator considering temperature compensation for 5G communication [J]. Analog Integrated Circuits and Signal Processing 118, 2024.

[28] Yandrapalli, Soumya, et al. Analysis of XBAR resonance and higher order spurious modes [J]. 2019 IEEE International Ultrasonics Symposium (IUS), 2019.

[29] Plessky, Victor, et al. Laterally excited bulk wave resonators (XBARs) based on thin Lithium Niobate platelet for 5GHz and 13 GHz filters [J]. 2019 IEEE IMS, 2019.

[30] Lin, Chih-Ming, et al. Micromachined aluminum nitride acoustic resonators with an epitaxial silicon carbide layer utilizing high-order Lamb wave modes [J]. IEEE International Conference on Micro Electro Mechanical Systems, 2012.